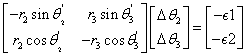This is an application of the Newton-Raphson method for finding the joint angles of a mechanism. This was adapted from a note I made in a class called Mechanics of Machines in my sophomore year. It has proven useful to me for numerous times since then. The Newton-Raphson method can be used on any closed-loop mechanisms, including non-inverted and inverted slider-crank mechanisms. It also converges relatively fast in many common cases which makes it such a convenient tool. Throughout the years the Newton-Raphson method one of my favorite tools as a ME student.
--
Consider the double-loop mechanism:
Link 1 is the input, i.e. the rotation angle of link 1 is specified. Since this mechanism have
one degree of freedom the positions of all other links can be found. Realizing that the two loops shown in the figure are in fact two four-bar linkages, we can solve them independently.
First of all, to find the joint angles of the 4-bar linkage made by links 1, 2, 3, and the ground link,notice that the vectors R
1, R
2, R
3, and R
6' have the following relationships:
$R_1+R_2-R_3-R_6=0$.
This is the loop equation for
Loop 1.
One must be aware of the direction of the vectors. Rewriting this equation in terms of link lengths r
1, r
2, r
3, r
6', and joint angles $\theta_1,\ \theta_2,\ \theta_3,$ and $\phi_6'$, it becomes:
$r_1\cos\theta_1+r_2\cos\theta_2-r_3\cos\theta_3-r_6\cos\phi_6=0$
$r_1\sin\theta_1+r_2\sin\theta_2-r_3\sin\theta_3-r_6\sin\phi_6=0$.
There are two unknowns, $\theta2$ and $\theta3$. The goal here is to find solutions to these two equations:
$F_1(\theta_2,\ \theta_3)=r_1\cos\theta_1+r_2\cos\theta_2-r_3\cos\theta_3-r_6\cos\phi_6$
$F_2(\theta_2,\ \theta_3)=r_1\sin\theta_1+r_2\sin\theta_2-r_3\sin\theta_3-r_6\sin\phi_6$
Here we will apply the Newton-Raphson method.
- Find estimated values $\theta_2$ and $\theta_3$. Let's call them $\theta_2'$ and $\theta_3'$.
- The partial differivative of F1 and F2 with respect to $\theta1$ and $\theta2$ are
$\frac{\partial F_1}{\partial \theta_2}=-r_2\sin\theta_2$, $\frac{\partial F_1}{\partial \theta_3}=r_3\sin\theta_3$
$\frac{\partial F_2}{\partial \theta_2}=r_2\cos\theta_2$, $\frac{\partial F_2}{\partial \theta_2}=-r_3\cos\theta_3$.
- Since the values are estimated, it is highly unlikely that they will be the exact solution to F1 and F2. That is, F1 and F2 will not be zero when substituting these values into the equations. We write:
$F_1(\theta_2',\ \theta_3')=\epsilon_1'$
$F_2(\theta_2',\ \theta_3')=\epsilon_2'$.
- Then Newton-Raphson method yields that
$-r_2\sin\theta2'\times(\Delta\theta_2)+r_3\sin\theta_3\times(\Delta\theta_3)=\epsilon_1-\epsilon_1'$
$r_2\cos\theta2'\times(\Delta\theta_2)-r_3\cos\theta_3\times(\Delta\theta_3)=\epsilon_2-\epsilon_2'$
where $\epsilon_1=\epsilon_2=0$ in this case (the cost of F1 and F2).
- Solving the equations in 4. gives the change for $\theta_2$ and $\theta_3$.
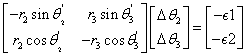
.
- The new estimation for the two values are $\theta_2''=\theta_2'+\Delta\theta_2$ and $\theta_3''=\theta_3'+\Delta\theta_3$, respectively. Using these new values we can start the process from step 3 and find new values again. The values will converge to the exact value of $\theta_2$ and $\theta_3$. Once the values are withing tolerance, the procedure is terminated and we had our answer.
The procedure for
Loop 2 is the same as that described above. Just use the Newton-Raphason method again to find $\theta_4$ and $\theta_5$.
 TGIF! What a nice day it was to go down to the local library and get some easy reading material. I heard about Fortunately, the Milk from Neil Gaiman's Tumblr (Nice marketing, Mr. Gaiman!), and had wanted to get my hands on one ever since its publication last month. Imagine my excitement when I found out that the library already have several copies and I can place a hold for one (They circulate fast and were all checked out.). Now imagine what it's like to finally get a message after a week's waiting:
TGIF! What a nice day it was to go down to the local library and get some easy reading material. I heard about Fortunately, the Milk from Neil Gaiman's Tumblr (Nice marketing, Mr. Gaiman!), and had wanted to get my hands on one ever since its publication last month. Imagine my excitement when I found out that the library already have several copies and I can place a hold for one (They circulate fast and were all checked out.). Now imagine what it's like to finally get a message after a week's waiting: Romance rarely top my list of enjoyable stories. Recall seeing lovebirds engage in passionate kisses with hands over the place at public places and make everyone present uncomfortable? The show off cannot compare to the sight of the couples holding hands with shyness and a hint of a smile lingering on both sweet faces. Love stories can be like that: Showy but unconvincing or subtle and sweet. When two people fell in love in a story, it should be believable. Let readers feel the love! The audience should not be merely the spectator. They should be engaged in a relationship.
Romance rarely top my list of enjoyable stories. Recall seeing lovebirds engage in passionate kisses with hands over the place at public places and make everyone present uncomfortable? The show off cannot compare to the sight of the couples holding hands with shyness and a hint of a smile lingering on both sweet faces. Love stories can be like that: Showy but unconvincing or subtle and sweet. When two people fell in love in a story, it should be believable. Let readers feel the love! The audience should not be merely the spectator. They should be engaged in a relationship..jpg) Casino Royale is the first James Bond novel by Ian Fleming. Instead of boring and tedious background stories, readers get to learn about the mysterious spy the way one would when making new acquaintances: We judge him by his actions and beliefs. The outcome was not bad. Even with a negative view, James Bond's emotions were easy to connect with. One can almost feel sentimental about his situations. To conclude, the book is believable and invites the reader to experience the thrill without the danger.
Casino Royale is the first James Bond novel by Ian Fleming. Instead of boring and tedious background stories, readers get to learn about the mysterious spy the way one would when making new acquaintances: We judge him by his actions and beliefs. The outcome was not bad. Even with a negative view, James Bond's emotions were easy to connect with. One can almost feel sentimental about his situations. To conclude, the book is believable and invites the reader to experience the thrill without the danger.
 Of Mice and Men is a novella
Of Mice and Men is a novella